By Ivana Bozic
Hello everyone! My name is Ivana Bozic (pronounced as “Bozhich”) and I am a new Assistant Professor in the Applied Mathematics department. I received my bachelors and masters degrees in pure mathematics from the University of Belgrade in Serbia, where I am from. After obtaining my masters, and realizing that I am more interested in applied than pure math, I moved to the US to do my PhD in mathematical modeling of cancer. I received my PhD degree in Mathematics from Harvard University and stayed there for my postdoc as well. I joined UW only a few months ago, in March 2017, and I am very excited to be here!
I study the evolution of cancer and its resistance to treatment through mathematical and computational modeling. My interests lie in both theoretical aspects of these models and their application. On the theoretical side, I study stochastic processes, especially multi-type branching processes, and their finite time characteristics. I collaborate extensively with experimental and clinical researchers to integrate modeling with clinical data, providing insight into the natural history of cancer in vivo.
In healthy tissues, cell division and cell death are tightly controlled processes, which enable a precise balance assuring that the number of cells in the body remains approximately constant. However, during each cell division mistakes in DNA replication can occur, leading to accumulation of mutations in individual cells. The majority of such mutations are effectively neutral (passengers), but some of them (drivers) can provide selective advantage to the cell, by tipping the balance of cell division and death in favor of increased proliferation. This unwanted evolution of somatic cells can lead to a clonal expansion of cells with driver mutations, which can ultimately result in the formation of tumors and seeding of new lesions in distant tissues. My approach combines developing and studying mathematical models of genetic evolution together with genomic data to obtain insights into these important, but hidden evolutionary processes.
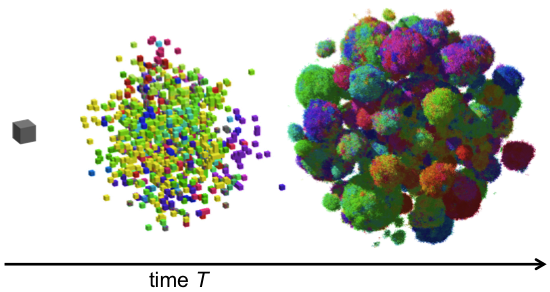
For example, in recent work we studied the genetic evolution of cancer in three-dimensional space. We were interested in how drivers and passengers accumulate in the presence of spatial constraints due to crowding and nutrient deprivation, which play a significant role in non-microscopic solid tumors. We also studied the effects of short-range dispersal on tumor growth, and our model suggested that targeting short-range cellular migratory activity could have marked affects on tumor growth rates. Our model not only provides insights into spatial and temporal aspects of tumour growth, but also suggests that targeting short-range cellular migratory activity could have marked effects on tumour growth rates.
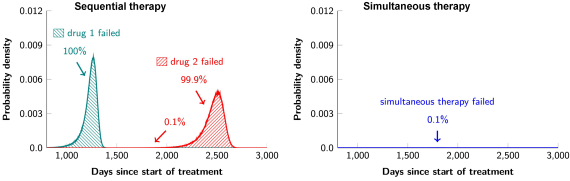
I am also very interested in studying cancer therapy through a quantitative lens. Combination targeted therapies are widely believed to be the one of the best hopes for achieving long-term remissions in cancer patients. In collaboration with cancer researchers from Johns Hopkins, we studied a mathematical model for the evolution of resistance to combination targeted therapy in order to critically evaluate the potential and limitations of such therapies in actual disease settings. We found that combination therapy will not lead to long-term disease control in most patients if there is even one possible mutation that has the potential to cause cross-resistance to the administered drugs. In other words, if any of the 6.6 billion base pairs in a typical diploid cell can be mutated to a form that causes cross-resistance, the effects of combination therapy will not be dramatically better than monotherapy. Moreover, even if there is no possibility of a mutation that could cause resistance to two drugs, dual therapy will fail in patients with large disease burdens. In such cases, triple therapy will be needed – and this will only be successful if there is no possibility that a mutation could cause cross-resistance to all three drugs. Finally, we demonstrated that the current practice of administering targeted agents sequentially is a recipe for certain treatment failure and that simultaneous administration of targeted agents is essential for long-term disease control.
In sum, cancer is the result of a stochastic process during which cells accumulate mutations that are responsible for tumor initiation, growth, dissemination to distant tissues and resistance to therapy. As such, mathematical modeling can help answer many important questions in cancer research, especially when working in close collaboration with experimentalists and clinicians.
