By Aleksandr (Sasha) Aravkin
Exactly a year ago, in August 2015, I joined the Applied Math department at the University of Washington as an Assistant Professor. My relationship with the UW began much earlier in 2000, first as an undergraduate, and then as a graduate student. My doctoral work, supervised by Jim Burke, developed robust formulations and optimization algorithms for dynamic inference. Concurrently, I obtained an M.S. in Statistics, and statistical modeling has since been central role to my work.
In 2010, I joined the Seismic Laboratory for Imaging and Modeling (SLIM) at UBC as a post-doctoral fellow. At SLIM, I worked closely with students and faculty from Earth and Ocean Sciences, Computer Science, and Mathematics departments to solve large-scale seismic inverse problems using statistical modeling, compressive sensing, and optimization techniques. In addition to learning a lot about inverse problems, I realized how fun it is to work with researchers in applied disciplines who have specific problems they really care about.
In 2012 I joined the IBM Watson Research Center as Research Staff. IBM Research has labs all over the world, but the Watson Research Center is the mothership, housing 1,800 researchers with expertise ranging from physics and chemistry to mathematics and machine learning. These researchers are distributed in a somewhat convoluted organizational hierarchy, but the culture and work environment makes it easy to work with colleagues across groups. While at IBM, I collaborated with researchers in machine learning, signal processing, optimization, inverse problems, weather modeling, indoor localization, computer vision, and speech recognition. I also worked on modeling projects for clients in the US, Netherlands and Brazil. I found I missed teaching and interacting with students, so I taught three masters-level machine learning courses as an adjunct professor at Columbia University. When I considered my long-term career goals, I realized I wanted to be in academia, and I was thrilled to get an opportunity to return to my alma mater.
Back at UW
Returning to the UW has been fantastic, both personally and professionally.
I am delighted to be a part of Applied Math – it’s a great feeling to personally know and regularly talk to all of my colleagues, and to be actively involved in decisions shaping the curriculum, growth, and development of the department. My position is shared with the eScience Institute, where I am also a Data Science Fellow. eScience is making a tremendous difference in interdisciplinary work, by bringing together experts in methods and applied domains to promote collaboration and education, especially in data science and data-driven discovery. It has also been a pleasure to continue ongoing collaborations with friends in Mathematics and Statistics, and I am very happy to be affiliated with both departments as an adjunct professor.
Research at UW
The greatest joy of coming to UW has been doing research with graduate students, who are remarkably strong, ambitious, and independent. I am currently advising two students, Peng Zheng and Jize Zhang, and working with many others on research projects (Kelsey Maass, Jonathan Jonker, and Xin Chen, who is advised by Doug Martin).
It’s a great time to be doing optimization at UW – among many distinguished faculty across campus who work on theory and algorithms, I have worked closely over the last year with Dmitriy Drusvyatskiy and James Burke in Mathematics. We have been collaborating on teaching, research, and curriculum design, and have ongoing projects with students in Math and Applied Math, including Courtney Kempton, Scott Roy, and Kellie Macphee (advised by Dima) and Abe Engle (advised by Jim). Many Amath faculty, including Randy LeVeque, Nathan Kutz, and Eric Shea-Brown, and their respective groups, are working on projects closely tied to machine learning and optimization, and I am always delighted to speak to them.
I have also continued and expanded my collaborations with colleagues at IBM, UBC, Padova, and Utrecht, and started new and exciting collaborations with Cornell. Coming to the UW has deepened my interest in structured optimization, with large-scale real-world applications motivating new theoretical analysis and algorithmic development. I am extremely grateful to the Washington Research Foundation (WRF) for supporting my research with the WRF Data Science Professorship.
A Sampler of Projects
Below are a few examples of research that I am very excited about. Since I’m generally very excited about all the projects I work on, these examples are biased towards those with interesting graphics.
Trimmed Robust Estimators for General Models
Development of robust formulations and anomaly detection are closely related goals for most learning and inverse problems. Unusual features, flipped labels, fraudulent transactions, and unmodeled data are all complicating features of learning and inversion. We want to make useful inference in spite of these issues, as well as precisely identify where they are coming from (i.e. who is committing fraud, which sources of data are unusually noisy, etc).
As a running example, consider the MNIST dataset, which is a set of hand-written digits used to train a multi-class classifier, to identify which digit (0, …, 9) a person has written.
Most learning problems can be formulated as minimizing a sum of a loss or likelihood over the available training examples. In the MNIST example, a training example is a 28 x 28 pixel image of a hand-written digit, together with a label indicating which digit it represents.
Trimmed estimators were proposed in the 1980’s for least squares regression. The general idea is to multiply each example loss or likelihood by a weight, ranging over the interval [0,1], and require that the weights add up to an estimate of ‘good’ data.
We can solve a joint optimization problem over these weights and parameters of interest. Any point whose weight goes to 0 over the course of the optimization is automatically labeled an ‘outlier’, and is (automatically) not considered in the training. Trimming is an elegant way to simultaneously robustify any formulation (by taking bad examples out), and identify the bad examples (simply by looking at their weights).
For a recent pre-print in the high-dimensional setting, please see: http://arxiv.org/abs/1605.08299
The following example is from an ongoing project with Damek Davis. What happens if we use the approach on the MNIST dataset, and declare that 99.8% of the data are good? We will find the most egregious outliers! Six are shown below.
Caption: Labels for these images are: ‘9’, ‘3’, ‘5’, ’9’, ‘4’, ’8’.
Seismic Data Interpolation
Geophysical exploration, reservoir characterization, and subsurface imaging are all examples of seismic inverse problems. These problems are extremely large scale: model parameters of interest are typically gridded parameter values over a 3-dimensional mesh. If your mesh has 1000 grid-points on each side, your inverse/optimization problem has a billion unknowns!
The most expensive part of geophysical exploration is data acquisition. For 3D seismic imaging, the acquisition process requires a 2D array of wave sources and a 2D array of receivers. Sources generate waves, and receivers pick them up; since waves travel in space and time, the data is arranged in a 5D seismic cube (2 dimensions for each source and receiver, and one dimension for time).
Using low-rank optimization formulations, we can interpolate 80% missing seismic data. Low-rank formulations are an important technique for recommender systems, such as the Netflix Prize problem. The insight from SLIM was to use a specific matricizations (unfolding) of the seismic data tensor, to discover low-rank structure in the data. We developed a custom algorithm to solve the problem. Some of the results are shown below.
Caption: (a) shows interpolated data, with 80% filled in. (b) shows the difference between original data and interpolated section, multiplied 100-fold. The approach recovers essentially all coherent information in the data.
For a preprint, please see: http://arxiv.org/abs/1607.02624
Piecewise Linear-Quadratic (PLQ) Modeling
A lot of large-scale learning problems can be formulated using non-smooth and asymmetric penalties.
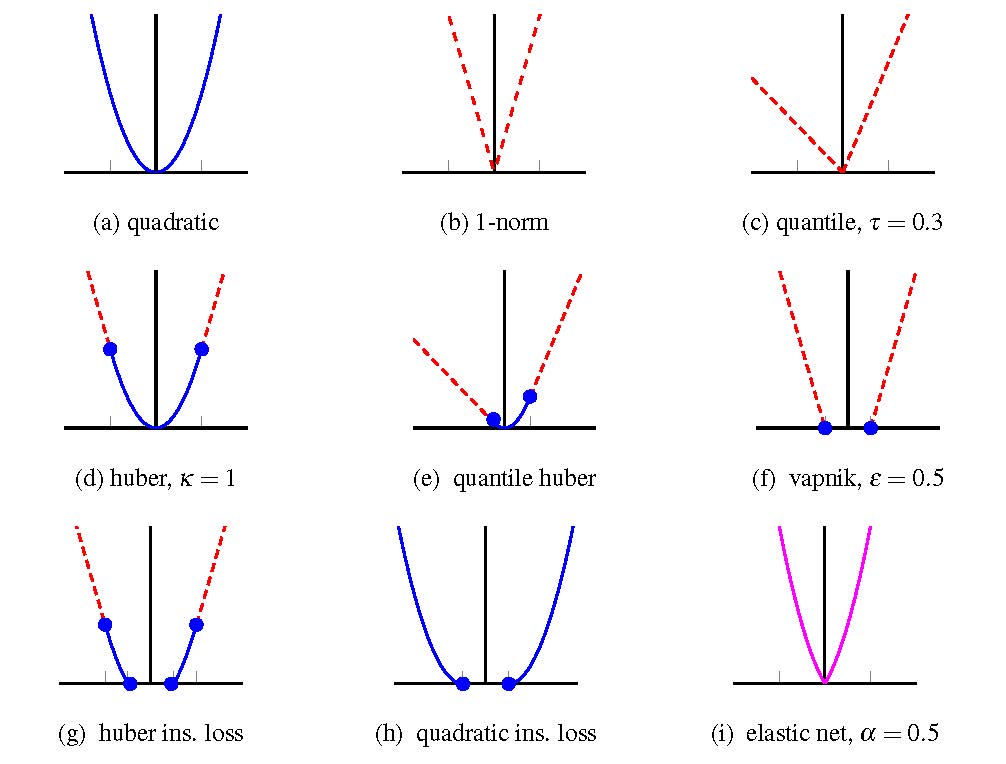
Figure 4 shows several examples. All of these penalties share a simple structure that can be used to design fast optimization algorithms, and can be applied to a variety of problems.
I maintain an open source IPsolve code that can solve general PLQ problems, with a growing number of examples:
https://github.com/saravkin/IPsolve
Primary reference: https://arxiv.org/abs/1301.4566
Recent extensions: https://arxiv.org/abs/1309.7857
Ongoing work includes faster optimization codes for large-scale PLQ problems and formulations and algorithms for nuisance (shape) parameter estimation.
Variable Projection
An interesting idea in optimization is that of partial minimization, also known in some contexts as ‘variable projection’. Given an optimization problem with a natural partition over the variables,
miniminize g(x,u)
we can often gain some advantage by thinking of the problem as follows:
minimize G(u), where G(u) = minimum over x of g(x,u).
For example, a seismic PDE constrained optimization problem may look like this:
minimize over (x,u) ||Px – b||^2 subject to A[u] x = q,
where x is a wavefield over the domain, b are observed data, u are unknown velocity parameters, A[u] is a discretized PDE operator with boundary conditions, and q denotes a source term. These problems have been thoroughly studied, and conventional wisdom suggests avoiding the following reformulation:
minimize over (x,u) ||Px – b||^2+ s ||A[u] x – q||^2,
However, by using the partial minimization technique (in particular minimizing over x), we can design and analyze and efficient practical algorithm, with applications to seismic imaging, boundary control, mass transport, and Kalman smoothing.
For a preprint, please see: https://arxiv.org/abs/1606.02395
For nonsmooth examples, see: http://arxiv.org/abs/1601.05011