By Eli Shlizerman
The last time that I wrote in AMATH UW Newsletter was in the 2015-16 academic year when I assumed a tenure-track Assistant Professor position in the departments of Applied Mathematics and Electrical & Computer Engineering. Since then, a lot of progress has happened in NeuroAI-UW, the research laboratory that I have established. One progress is the promotion of my position from Assistant Professor to Associate Professor with tenure, starting this academic year. In appreciation of the occasion, I would like to take the opportunity and update you on the thrilling developments in my research and to provide an outlook ahead.
What is NeuroAI?
We are in the midst of a computational revolution in which the notion of computing is being redefined by Artificial Intelligence (AI) systems. These are generic systems capable of computing ubiquitous tasks by learning from data. In other, more technical words, AI systems employ optimization of their inner parameters, a.k.a training, to map a variety of inputs to outputs. In the process of training, the systems converge to a representation of the mapping. At the end of training, the systems employ the representation to accurately map unseen inputs to appropriate outputs.
The advantage of such systems is that their setup is generic. In principle, a similar system can be trained to recognize objects in videos, and with only a few changes, to translate sentences from one language to another. The genericity is due to them being composed of computational units called ‘neurons’, organized in a network with a layered architecture, hence their name Deep Neural Networks. While computational neurons are simplified versions of physiological neurons in the brain, and the interaction between neurons is different in the two networks, deep neural networks and neurobiological networks share common principles.
Why is NeuroAI Needed?
Beyond sharing common principles, deep and neurobiological neural networks complete each other. Neurobiological Networks have been shaped by evolution to form pathways for the flow of information from sensation to behavior, i.e., the overall architecture - Connectome (the connectivity of neurons) of neurobiological circuits is set to map stimulus to neural dynamics, and then to function (behaviors) (top row in red in Figure 1). Hence we can learn from the Connectomics structure how networks of neurons are designed for various functions. Further, since neurobiological networks are high dimensional nonlinear systems, we can investigate how physiological neurons and Connectome merge together to generate dynamics along with output mappings to represent behaviors.
In Deep Neural Networks, the information flows in the inverse direction. The desired function (output) of the network is given, and data samples of this function are given too. However, it is not known how neurons will represent the task and it is not known how neurons will be connected to each other (connectivity weights). Training completes these unknowns, in particular, the connectivity weights, through optimization of input-output similarity. Hence we can learn from investigation of deep neural networks how the representation is being self-organized and what is the space of possible representations. We can further investigate what are the principles of neural networks, questions such as: When can we expect the optimization to converge? Can we predict the accuracy of the networks?
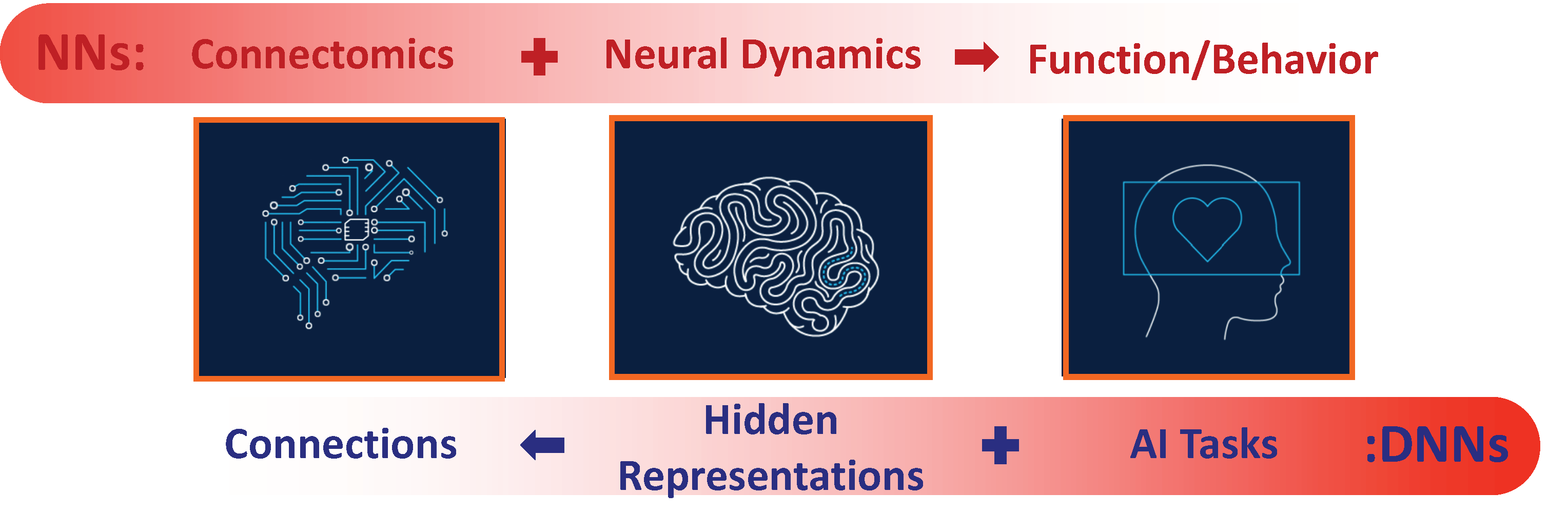
Figure 1. Complementary pathways of computing in neurobiological networks (top) and deep neural networks (bottom).
Our Advances in NeuroAI
The development of novel mathematical methodologies for interfacing Nero (NN) and AI (DNN) systems to studying them jointly holds the potential to close fundamental gaps in both systems. Below I describe and provide examples of the advances that we have achieved.
Interpretation of neural activity (NN): Neurons represent information through dynamic activity. Such activity can be recorded with various technologies. There is rapid progress in the effectiveness and the number of neurons that simultaneously can be recorded. With these developments, an imminent problem arises: how do we analyze and interpret these recordings and correlate them with stimulus? We are developing data-driven methods to address this problem. The methods interface several computational areas such as machine learning and dynamical systems, and translate multidimensional time series into mathematical objects such as Clustering Embeddings, Classification Spaces, and Casual Graphs (see Figure 2).
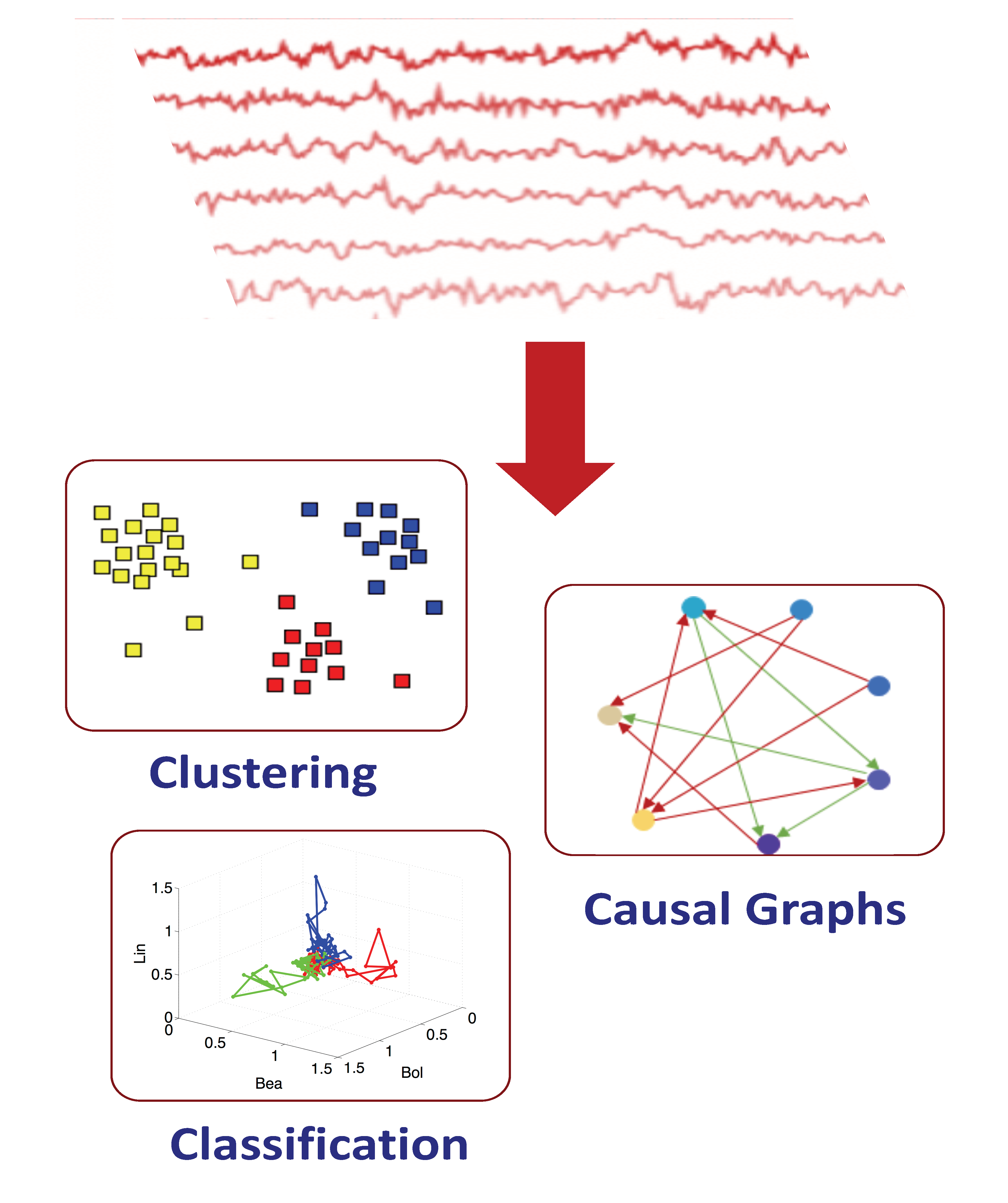
Figure 2. From neural dynamics to representations.
Attractors represent classes of functions (NN) or classes of tasks (DNN): Successful construction of such objects, e.g. low-dimensional neural classification phase spaces, correspond to proxies for interpretation of the recordings. For example, neural classification space can map neural dynamics into attractors representing distinct stimuli or behaviors (Figure 3 left). We applied tools that we developed to various recordings such as recordings from projection neurons in the antennal lobe of tobacco hornworm moth, to directional neurons in the Monarch’s central complex, to artificial neurons monitoring `Crowdsensing’ of pollutants in the environment [1,2,3,4,5].
Representation of functions is not proprietary to neurobiological networks and neurons. We analyzed the hidden (latent) states of Recurrent Neural Networks (deep neural networks that process time series) and applied similar tools to study their latent representations. We found embeddings onto which projections of the network latent states show that the network effectively performs dimension reduction consisting of only a small percentage of dimensions of the network hidden units. Furthermore, sequences are being clustered into separable clusters in the embedded space, each of which corresponds to a different type of dynamics (Fig. 3 right). Such clustering property is self-emerging and we proposed to use it for the design of state-of-the-art unsupervised action recognition exceeding the performance of many supervised methods [6,7].
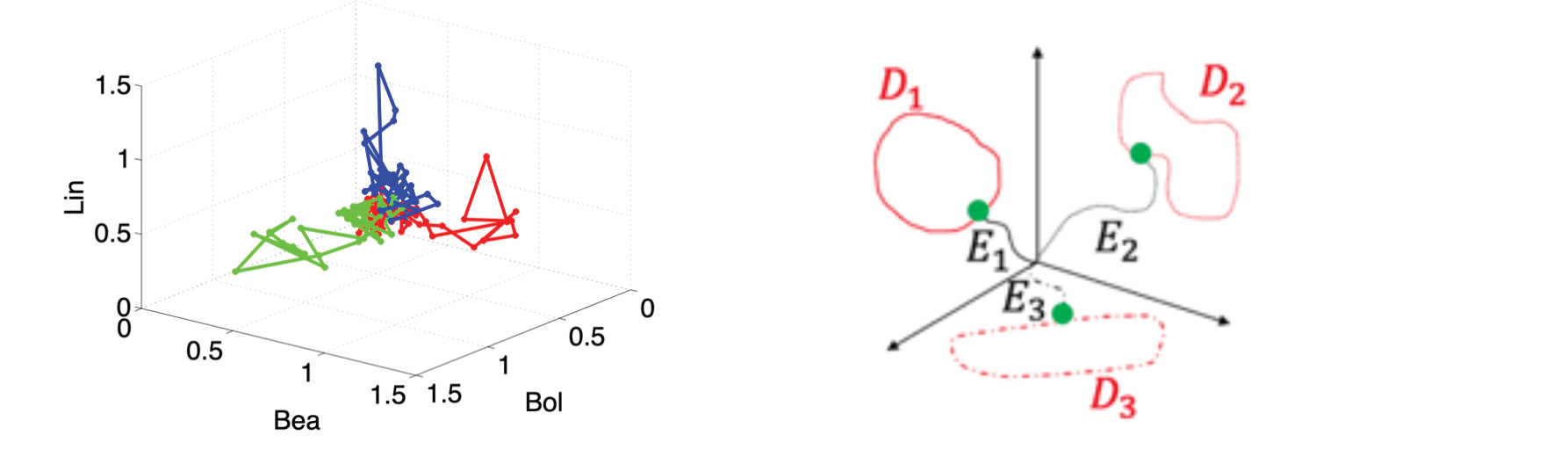
Figure 3. Data-driven low dimensional embeddings reveal how multi-neural dynamics in neurobiological networks (left) or latent neural dynamics in recurrent neural networks (right) mapped to attractors, each of which correspond to a stimulus (left) or a task (right).
Novel capabilities for AI systems (DNN):. With novel applications, we are exploring how deep recurrent neural networks encode and decode continuous signals and whether they can capture correlations between subtly related sequences. For example, our work named ‘Audio to Body Dynamics’, showed that such networks can capture the transformation from music to movements and to predict the coordinates of a musician’s fingers exclusively from the sound signal. Recently, in a project named ‘Audeo’, we showed that it is also possible to perform an inverse task and to generate music from movements. Furthermore, in an additional application, named ‘Predict & Cluster’, we showed that a special architecture, Seq2Seq, can be applied to a high-accuracy clustering of human body actions, a challenging problem, particularly in an unsupervised learning setting [7,8,9,10].
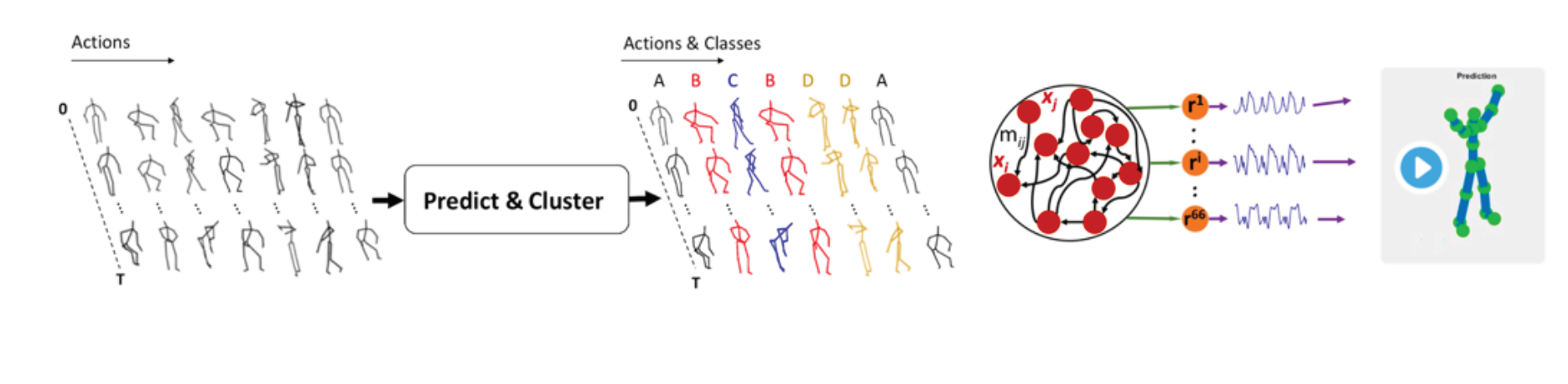
Figure 4. Left: Predict & Cluster: unsupervised activity recognition based on latent representation of RNN trained for prediction. Right: Generating body movements in 3D (66 coordinates) with Robust-FORCE Learning.
Recovery of connectivity (NN): A major application for recorded neural activity datasets is the recovery of a map that specifies how the information flows within NNs and how neurons could be wired to generate such data. The problem originates from the fact that recordings of neural activity are realizable, while tracing connections or estimating neural interactions is challenging. We introduced methods for solving such inverse problems: recovery of ‘guaranteed’ networks to generate the recorded data (rigorously proved) and inference of ‘effective’ wiring (causal connectivity). These methods aim to extend the dynamical system theory to include ‘dynamical systems with constraints’ and adapt the methodology of inference of causality graphs to high-dimensional spatiotemporal data.
Predictive modeling (NN): How does the connectivity structure (connectome) is merged with biophysical processes to shape the activity of the nervous system and associated behaviors? Extensive data is available only for model organisms. We collaborate with experimentalists on detailed, realistic as possible, predictive modeling for such model organisms. Specifically, we are developing large-scale differential equations simulations to model connectomes with biophysical neural properties. Such a platform makes it possible to generate full nervous system activity along with behavior and serves as an innovative framework for generic perturbative methods to analyze ensembles of neural activity with behaviors. We have demonstrated the application of the platform to the nervous system and the neuro-mechanics of the nematode Caenorhabditis elegans by developing a detailed in silico model of its nervous system and have introduced novel methods for inference of sensorimotor pathways within the nervous system [11,12,13].
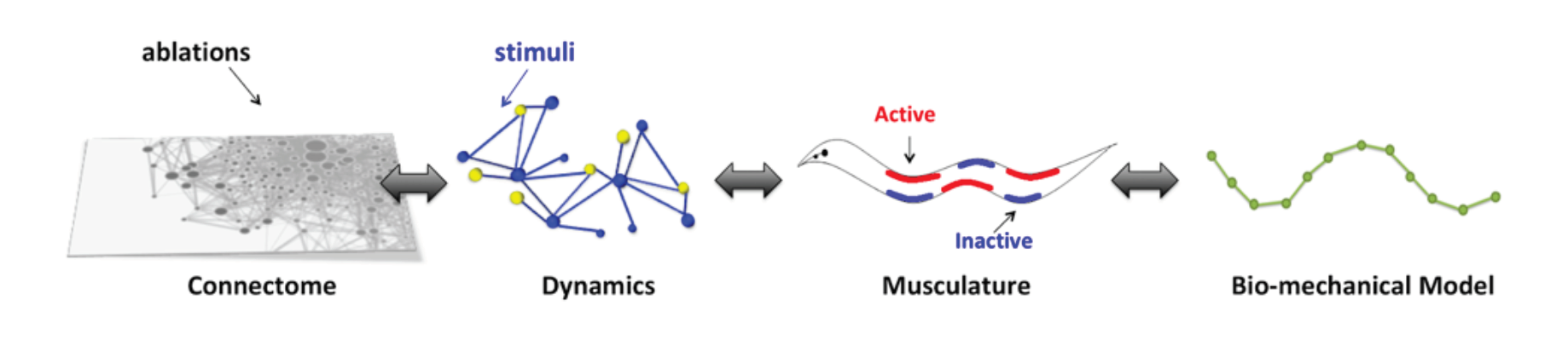
Figure 5. Predictive model of the nervous system and body of C. elegans for the study of interaction of connectome, neural activity and behavior.
The Future of NeuroAI
Our work has shown the prospect of extending dynamical systems theory and data-analysis methods as a synergistic study of NN and DNN systems. Furthermore, it demonstrates that known attributes in one type of systems lead to important developments in the other type. These are indicators that bringing the two systems together would pave the way toward universal computing with neurons – given an appropriate intelligent task, it would be possible to generate, in a systematic way, a network of neurons which computes this task.
While nervous systems show that neurons are powerful computing entities and while DNNs demonstrate competence to perform intelligent tasks, currently, there are gaps pertaining to the establishment of fundamental rules of computing for both systems. Our current and future research is aimed to fill-in these gaps and to establish theoretical and practical concepts for neural network computing. In particular, our investigations are multipronged studies addressing the structure, control, and learning foundations of neural networks:
- Structure – Investigation of NNs connectomes and the design of novel methods for connectome generation in vivo and in DNN systems [14].
- Control and Performance - Development of methods to achieve balanced, stable and robust networks for generic computing of various tasks [15].
- Learning – Transferring the concepts of learning in NNs to DNNs.
The Role of (Applied) Math in NeuroAI
In summary, in the NeuroAI-UW lab we are developing novel methods combining analysis of spatiotemporal data, machine learning, and dynamical systems for the synergistic investigations of neurobiological and deep neural networks to advance our understanding of underlying mechanisms of neural networks computing. Applied Mathematics has always been leading research in these fundamental methods, and thereby, it is one of the natural disciplines to be at the forefront of research of fundamentals of neural networks.
Multiple courses at UW AMATH that my colleagues and I are teaching are a valuable resource to acquire background and to get involved in NeuroAI research. In addition, regular seminar activities, such as the NeuroAI UW seminar, that my students and I are running, with additional activities at UW CNC (Computational Neuroscience Center) will provide a quick step into this emerging research area in Applied Mathematics. You are more than welcome to attend these activities and to reach out to me for further information.
References (Selected)
[1] Riffell, J. A., Shlizerman, E., Sanders, E., Abrell, L., Medina, B., Hinterwirth, A. J., & Kutz, J. N. Flower discrimination by pollinators in a dynamic chemical environment. Science, (2014).
[2] Shlizerman, E., Riffell, J. A., & Kutz, J. N. Data-driven inference of network connectivity for modeling the dynamics of neural codes in the insect antennal lobe. Frontiers in computational neuroscience, (2014).
[3] Blaszka, D., Sanders, E., Riffell, J. A., & Shlizerman, E. Classification of fixed point network dynamics from multiple node time series data. Frontiers in neuroinformatics, (2017).
[4] Shlizerman, E., Phillips-Portillo, J., Forger, D. B., & Reppert, S. M. Neural integration underlying a time-compensated sun compass in the migratory monarch butterfly. Cell reports, (2016).
[5] Liu, H., Kim, J., & Shlizerman, E. Functional connectomics from neural dynamics: probabilistic graphical models for neuronal network of Caenorhabditis elegans. Philosophical Transactions of the Royal Society B, (2018).
[6] Su, K., Liu, X., & Shlizerman, E.. Clustering and Recognition of Spatiotemporal Features through Interpretable Embedding of Sequence to Sequence Recurrent Neural Networks. Arxiv (Frontiers in AI), (2020).
[7] Su, K., Liu, X., & Shlizerman, E.. PREDICT & CLUSTER: Unsupervised Skeleton Based Action Recognition, to appear in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2020).
[8] Shlizerman, E., Dery, L., Schoen, H., & Kemelmacher-Shlizerman, I. Audio to body dynamics. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), (2018).
[9] Zheng, Y., & Shlizerman, E.. R-FORCE: Robust Learning for Random Recurrent Neural Networks, Arxiv, (2020).
[10] Su K., Liu X., Shlizerman E.. Audeo: Audio Generation for a Silent Performance Video. NeurIPS, (2020).
[11] Kunert, J., Shlizerman, E., & Kutz, J. N. . Low-dimensional functionality of complex network dynamics: neurosensory integration in the Caenorhabditis elegans connectome. Physical Review E, (2014).
[12] Kim, J., Leahy, W., & Shlizerman, E. Neural Interactome: Interactive Simulation of a Neuronal System. Frontiers in Computational Neuroscience, (2019).
[13] Kim, J., Santos, J., Alkema, M.J., Shlizerman, E. Whole integration of neural connectomics, dynamics and bio-mechanics for identification of behavioral sensorimotor pathways in Caenorhabditis elegans, BioArxiv, (2020).
[14] Shlizerman, E. Driving the connectome by-wire: Comment on “What would a synthetic connectome look like?”. Physics of life reviews, (2019).
[15] Kim J., Shlizerman E.. Deep Reinforcement Learning for Neural Control. Arxiv, (2020).
