By Konstantinos Mamis
It was the fall of 2006 in Athens, Greece; and for me the last year of high school had just begun. Having chosen to apply to engineering schools for university studies, one of the main courses I had to take was Physics, and the first chapter of our textbook was on mechanical oscillations. There, an eerie old photo in black-and-white showed a tall suspension bridge that collapsed in 1940 due to aeroelastic flutter, an oscillatory bahavior caused by wind loads: It was Tacoma Narrows Bridge. Back then, it seemed to my 17th-year-old self that this bridge was at the end of the world, in a land so strikingly different from the place I was living in at that time. Now, 18 years after and at the beginning of my third year here in UW Applied Math, Tacoma Narrows Bridge is not in a semi-mythical location for me anymore; the new bridge is just on the route to Gig Harbor, a picturesque maritime city so typical of the greater Seattle area. And now that I’m thinking of it, the pleasant landscape and weather here in Seattle -especially this time of the year- resembles a lot that faraway place which is now Athens.
Without boring you with too many details, that knowledge of mechanical oscillations -along with knowing a few other things on calculus, chemistry and biology- paid off, and I got accepted in the National Technical University of Athens. The topic of my undergrad studies was Engineering, and in particular Naval Architecture and Marine Engineering. However, I always gravitated towards Applied Math: I was fascinated by the truly emancipating power of mathematics to elegantly model and safely predict real-life phenomena. What is more, Applied Math has this overarching ability to apply the same mathematical concepts and tools to systems from fields so different from one another, such as engineering, economics or biology. For this reason, I finally left my alma mater in May 2020, just after the end of the first COVID-19 lockdown in Greece, having successfully defended my PhD dissertation in Stochastic Dynamics. Deciding to specialize in this topic was the result of my realization early on as a master’s student that randomness is inherent in most applications; thus, the quantification of uncertainty is indispensable to any attempt of realistic modeling of physical or biological phenomena.
Despite how it feels when you are conducting research as a PhD student, getting your PhD is not the end goal; it’s just the beginning of your endeavors as a researcher -there is surely room to grow further in knowledge, and, more importantly, to mature. For me personally, the goal after my PhD was to dedicate myself to a particular field of applications where I would perform stochastic modeling; it was essential to change my modus operandi from developing math tools per se to be application-driven, that is, to do whatever it takes mathematically to solve a particular question pertaining to a real-life problem. The field to focus on should be both interesting to me and to a broader audience too -ideally resulting in work that would contribute to the common good. And of course, on a practical note, people already working in the field should be positive in giving the opportunity to a newcomer to work with them.
This opportunity was given to me here, in the States, starting from my first postdoctoral appointment for a year in NC State, Department of Mathematics in Raleigh. There, I’ve worked with stochastic epidemiological models that describe, among other diseases, the spread of COVID-19. Randomness enters into the compartmental models of epidemiology because model parameters are subject to uncertainties, arising from the variation of social and biological factors among individuals. Among the model parameters, contact rate is the most volatile, due to its strong dependence on the social activity that varies from person to person, and also changes over time. Uncertainties in contact rate are usually modeled as stochastic fluctuations around a mean value; what we’ve found is that it is crucial to incorporate temporal correlations to the said fluctuations, accounting for the existence of patterns in our social behavior. Without temporal correlations in the randomly fluctuating contact rate, models significantly underestimate the severity of the disease outbreak, see Fig. 1 for the Omicron wave of COVID-19 pandemic in the US.
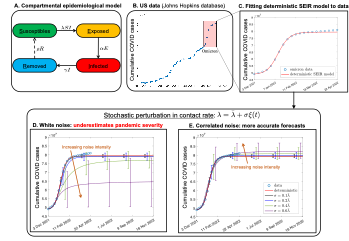
Figure 1: Summary of stochastic modeling and results for the Omicron variant of the COVID-19 pandemic in the US. (link to larger image)
I was able to continue working and deepening my understanding in mathematical biology thanks to the opportunity given to me by UW Applied Math, and my mentor Prof. Ivana Bozic especially. In my current position as a Pearson Fellow, I’m working on the fascinating topic of mathematical oncology; there, randomness is inherent in the process of mutation acquisition resulting in cancer, as well as the growth of cancerous and precancerous tumors.
Focusing on colorectal cancer, we first developed a stochastic population model for the cells residing inside each colonic crypt. Colonic crypts are the basic units of the inner intestinal surface; under healthy conditions they homeostatically maintain their size by employing a hierarchy of three cell types: a small number of stem cells in the bottom of each crypt giving rise to transit-amplifying (TA) cells, which after some rounds of divisions mature into the non-dividing fully differentiated (FD) cells. Colonic crypts are also the starting point of colorectal tumorigenesis, via the acquisition of cancer driver mutations by their stem cells. Our stochastic model is simple enough to be solved analytically, with its solution being in agreement with data from healthy crypts. For mutant crypts, our model correctly predicts the increase in size observed in crypts harboring the APC and KRAS mutations, the most significant early alterations leading to colorectal cancer.
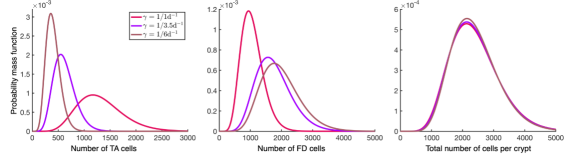
Figure 2: Crypts can maintain homeostatic size distribution under varying cell turnover rates γ. (link to larger image)
Furthermore -and perhaps more importantly- the mathematical model can inform us about the dynamics of the biological system at hand: For example, our model predicts a simple condition for the unbounded growth of cells in a crypt, corresponding to colorectal malignancy. It also shows that a hierarchy of three type cells can efficiently maintain the crypt homeostasis in cases of rapid cell turnover: crypt size distribution remains effectively unaltered when cell turnover increases, with the crypts responding by increasing their number of transit-amplifying cells; on the other hand, if cell turnover is slow, the tissue homeostasis can in principle be maintained by a two cell-type hierarchy (Fig. 2).
Another cancer-related project we are currently working on is to understand the mechanism by which the presence of tumors in early-stage cancer affect the levels of DNA fragments not bound to cells (called cell-free DNA) that can be detected in blood circulation. Cell-free DNA is a promising biomarker for early cancer detection, and knowledge on how it is shed and subsequently clear from the blood can potentially be useful in improving the accuracy of liquid biopsies. As in previous biological examples that we’ve mentioned, the main challenge in cell-free DNA modeling is its volatility, since cell-free DNA levels in a patient can be affected by various factors, such as physical exercise.
All projects I’ve mentioned in this piece are indicative examples of our way of working in mathematical biology: we are employing math models to provide insight into the biology with implications for preventive, diagnostic or therapeutic strategies; paraphrasing V.I. Arnold’s famous saying, mathematics is the part of science where experiments are cheap.
