I would be lying if I told you the reason I came to the University of Washington was anything other than the incredible mountains just outside the city. But besides these geographic charms, it was clear that the UW was also an excellent engineering school set in a diverse, cool city. In the end my choice was a no-brainer.
I arrived in Applied Mathematics without any clear research plan. My master’s research in Vermont had been in computational social science and networks, which isn’t part of our department’s offerings. So, for the first year, I focused on my classes and was frequently distracted by the copious snowfall that hasn’t really returned in the three years since. But Professors Eric Shea-Brown and Ioana Dumitriu, with whom I met regularly to get to know their research, both offered project ideas that I found interesting. Eric studies computational neuroscience, the use of mathematical tools to model and understand brain function. Ioana researches the spectral theory of random graphs, where the geometry of these random objects gives rise to matrices with particular algebraic properties. Both of their projects were interesting and new to me, and they would allow continued study of networks from a novel perspective.
Eric and I spoke with Nino Ramirez, Professor of Neurological Surgery, at a talk where he described experiments and modeling of a brain area that controls our breathing rhythm. We realized that we could extend his model to more complicated networks and study the effects of network structure as well as different cell types. In the years since, we’ve come to a better understanding of the role of inhibitory cells in the respiratory center. We know these cells are there, but the literature isn’t settled as to their purpose. With computational models, we can perform impossible experiments where we rewire connections at will or add and remove cells. Using this approach, we predicted that strengthened inhibition should lead to less synchrony among the cells and a weaker, more irregular rhythm. Working with our experimental collaborators, we then designed possible experiments with mouse brainstem slices to test this prediction and found it to be true, although we also found that our model was wrong in other ways. The give and take between experimental and theoretical sides of the collaboration is immensely satisfying for everyone involved.
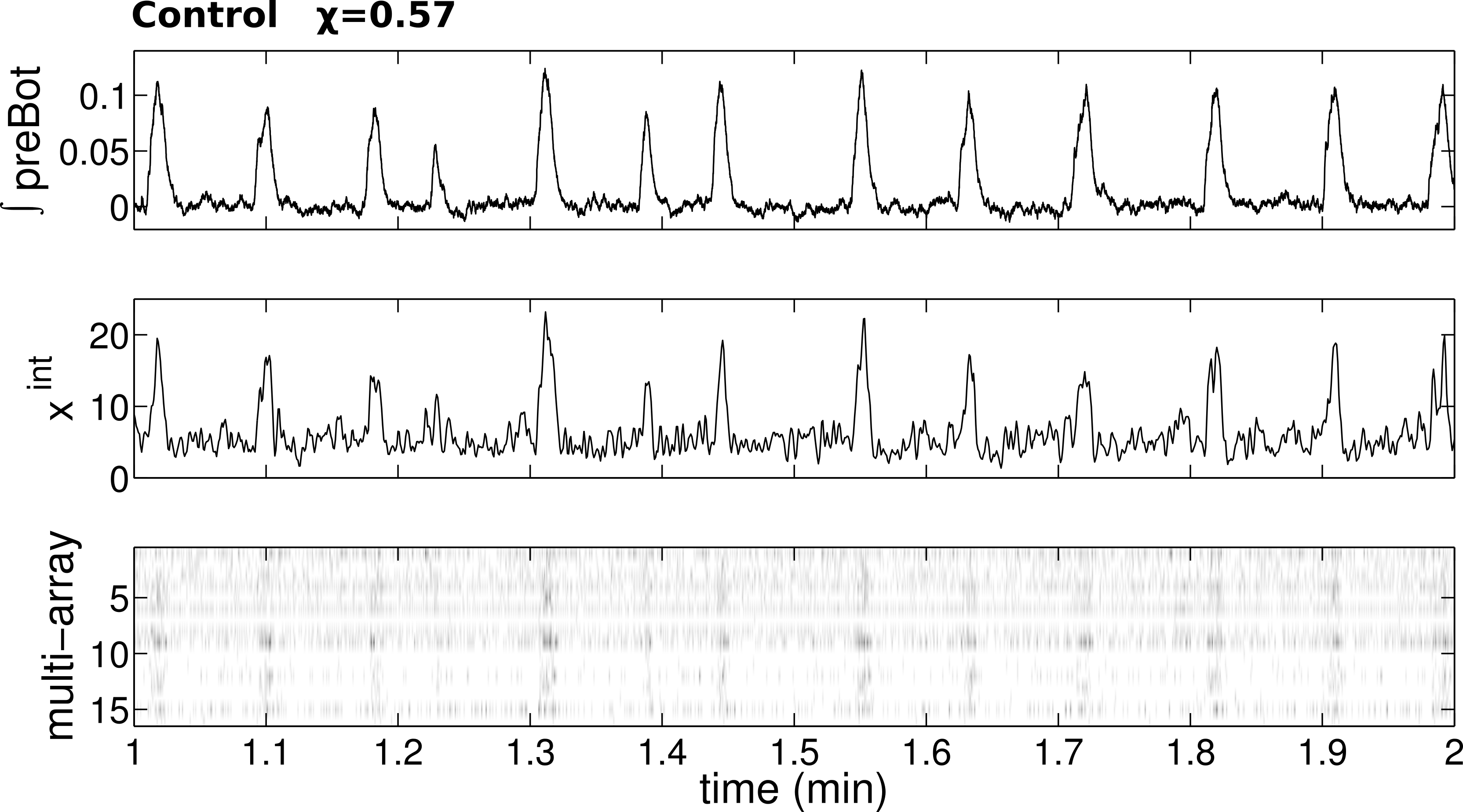
An experimental recording from the pre-Bötzinger complex, the brain area that regulates breathing. Top: rhythmic activity of the entire area. Bottom two: individual neuron activity and its neuron-by-neuron average.
Sometime along the way, Eric started meeting regularly with scientists at the Allen Institute for Brain Science and bringing his students along. There, I found out about their project to map the connectivity of the whole mouse brain. They’d been able to put together a matrix describing the connection strength between a couple hundred brain regions, but more data was coming in every day, and it was available in a much higher resolution than the level of regions. We started meeting, along with Stefan Mihalas of the Allen Institute, and my notebook filled up with ideas.
After a number of false starts, I eventually stumbled across an idea of a different shade, which didn’t assume anything about the unknown connectivity except that it varied smoothly as a function of position. We realized that smoothness would solve a number of problems: It was computationally tractable, filled in the gaps in our data, and was probably justified at the spatial scale we were considering. Now we’ve actually applied this method to data from the mouse visual system, and we’ve found that it does a better job inferring the connectivity than an earlier, state-of-the-art method.
These projects have ended up forming the core of my thesis research, supplemented by smaller projects with other collaborators, including random graph work with Ioana. Summer schools have taken me to Berkeley and Woods Hole, and I’ll spend a few weeks in Friday Harbor this summer, which I hope leads to an orca sighting. For conferences, I’ve traveled to exotic places like Banff, Little Cottonwood Canyon, and Pittsburgh. But there have also been challenges, like wrestling with undocumented data and code, frustration at the realities of coursework after a hiatus, feeling like my work is getting nowhere because I went from publishing regularly before my PhD to zero papers since entering a new field, or breaking an ankle while climbing and missing an epic Spring ski mountaineering season. We expect to be frustrated occasionally, but it’s still hard.
I’d like to end up in a job which uses the math I’ve learned, with colleagues who have fun together at work, and allows for time for my friends and family. I am happy that I’ve learned new math and a whole lot of biology and neuroscience. These skills can translate to a number of different careers, and I’m looking forward to the next exciting opportunity. Luckily, you can always find “skiing” somewhere in Washington.

Hiking out of Mt. Anderson on day 3 of a 4 day trip. Only 13 miles to the car! May, 2016.
