By Tim Leung
Last summer, I joined UW Applied Math as an Associate Professor and became the Director of the Computational Finance & Risk Management (CFRM) Program. Previously, I had been an Assistant Professor in the Department of Industrial Engineering & Operations Research at Columbia University in New York City (2011-2016) and in the Department of Applied Mathematics & Statistics at Johns Hopkins University (2008-2011), where I was heavily involved with their MS and PhD programs in Financial Mathematics/Engineering. I’m very excited to lead the UW CFRM program. Building on the program’s early successes, I will be working very hard with the AMath faculty and staff to assist our students to achieve their academic & career goals and help the program reach new heights in years to come. This year, CFRM has just climbed in the national ranking to #12 from #14 — a very motivating start!
My research area lies in Financial Mathematics & Engineering, which is ever-evolving multidisciplinary field with many interesting mathematical problems and countless practical applications. Hence, my research projects are often inspired by financial innovations, market phenomena, regulatory changes, and new analytical & computational methodologies. I have worked on a variety of problems, starting from my doctoral work on credit risk and executive stock options at Princeton University over a decade ago to my current projects on algorithmic trading and exchange-traded funds (ETFs).
Optimal Mean Reversion Trading
Market observations and empirical studies suggest that many asset prices exhibit mean reversion, including commodities, volatility indices, and equities. In industry, fund managers and traders often construct mean-reverting prices by simultaneously taking positions in two highly correlated or co-integrated assets (i.e. pairs/spread trading). On the other hand, one fundamental problem commonly faced by individual and institutional investors is to determine when to open and close a position, or multiple positions. This motivates the mathematical investigation of the optimal sequential timing of trades.
In a series of papers, my co-authors and I analyze a number of trading problems for different asset classes under various stochastic models with mean-reverting price dynamics. Our approach employs optimization and statistical techniques to construct the most mean-reverting portfolio, and then solves coupled optimal stopping problems or nested variational inequalities to determine the optimal times to enter and subsequently exit the market. Much of our work on this topic and some related problems has also been summarized in our recent book titled Optimal Mean Reversion Trading: Mathematical Analysis and Practical Applications.
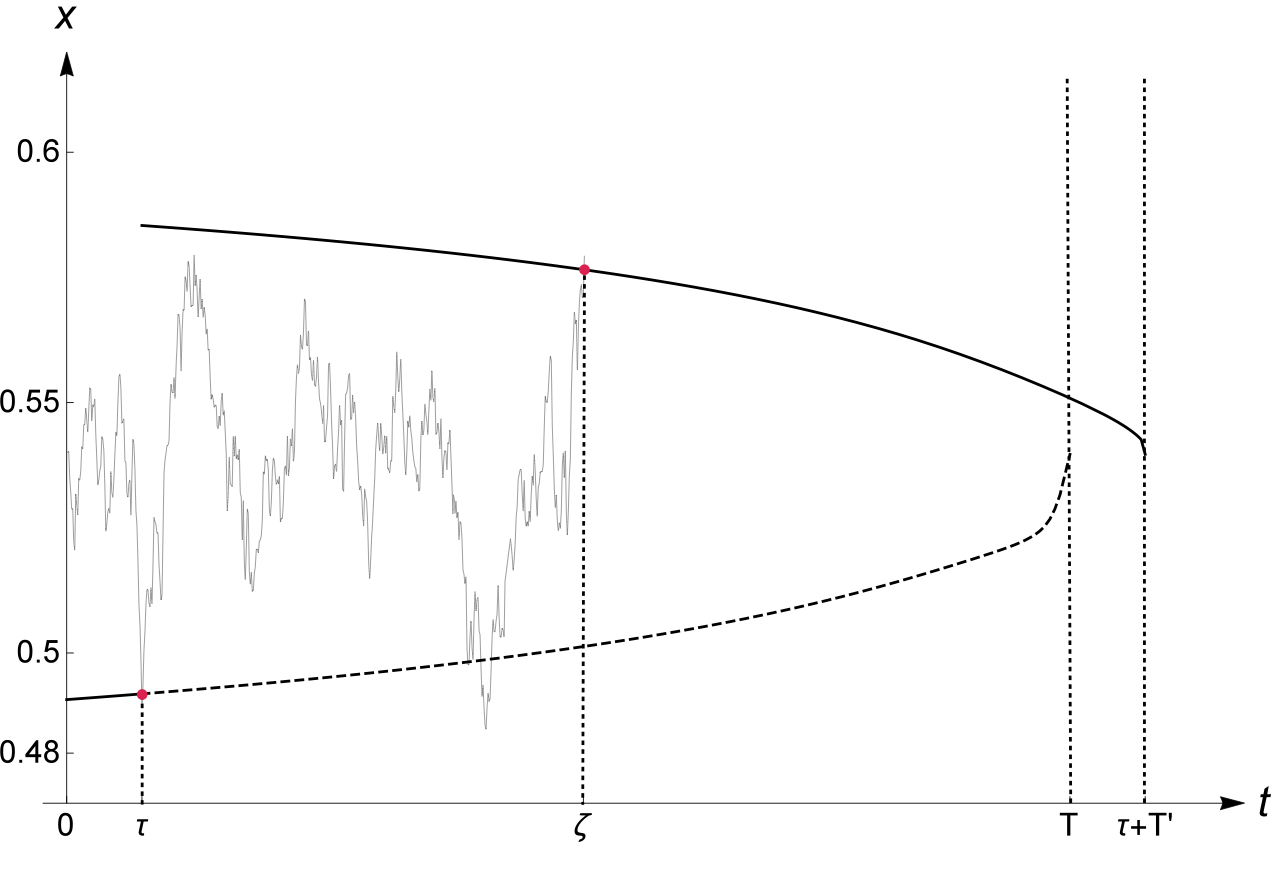
Fig. 1: A sample path of a mean-reverting price process. The trader enters the market as soon as the price hits the lower optimal entry boundary, and later exit the market when the price reaches the optimal upper exit boundary.
Exchange-Traded Funds
ETFs are relatively new financial products and have gained popularity in recent years. The ETF industry now consists of more than 1,600 funds with over $2 trillion in assets. All ETFs are traded on major exchanges like stocks, and most are designed to track an index or asset. Within the ETF universe, some funds are designed to replicate a constant multiple (called leverage ratio) of the daily returns of a reference index. These new financial products are called leveraged ETFs (LETFs), and the most common leverage ratios include {+3, +2, -2, -3}. As such, LETFs offer investors easy access to trade in different asset classes with positively/negatively leveraged exposures without borrowing.
The proliferation of ETFs has generated a host of new research problems. For instance, how well do these funds track their advertised benchmarks? Is there a mathematical connection between an (L)ETF and its reference index? What is the best trading strategy for tracking a given index? In my recent papers with students, we investigate the tracking performance of a wide array of equity and commodity LETFs and find that commodity LETFs tend to underperform compared to the theoretical benchmark. We also construct a dynamic leveraged portfolio using short-term futures, and demonstrate that this portfolio tracks the benchmark better than the market-traded LETF over a long out-of-sample period.
The use of ETFs and LETFs has also led to increased trading of options written on these funds. For (L)ETFs that track the same reference index, their associated options have very similar sources of randomness. This gives rise to the question of consistent no-arbitrage (no-free-lunch) pricing of options on ETFs and LETFs. To this end, my AMath colleague Matt Lorig and I study the mathematical connections among the implied volatilities derived from options prices on leveraged and unleveraged ETFs. Under a general stochastic volatility framework, we develop analytical approximations and numerical methods to price LETF options and derive mathematical formulae for price comparison across different options markets.

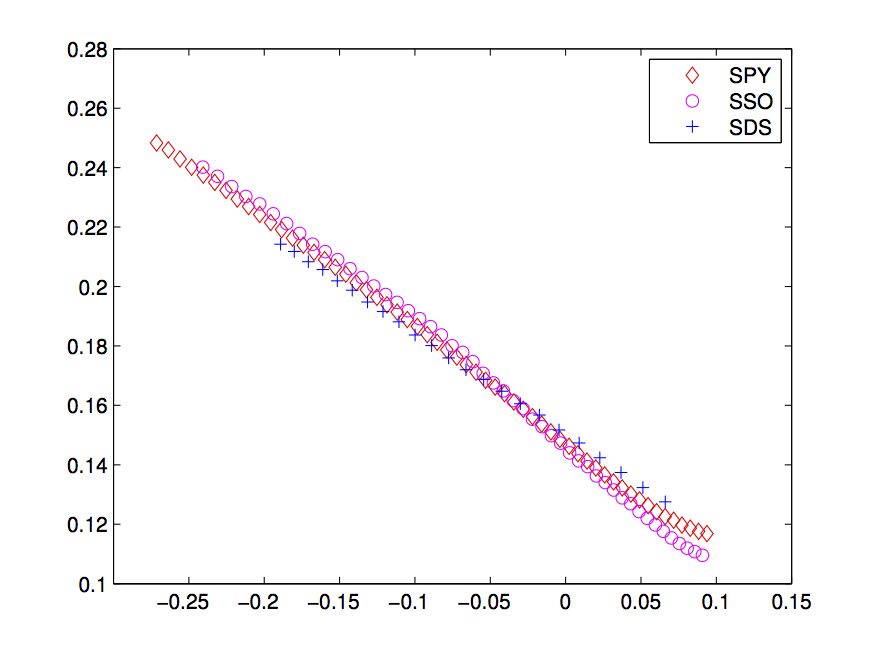
Fig. 2: The implied volatilities of options written on the S&P500 ETF (SPY) and its leveraged counterparts, SSO (+2x) and SDS (-2x). At first look, they look unrelated (left panel). After a mathematical scaling, we can line them up for direct comparison (right panel).
In retrospect, my research on LETFs was first motivated by an alert issued by the U.S. Securities and Exchange Commission regarding the riskiness of LETFs, along with news articles on ETFs and my empirical observations. Looking forward, as the market of ETFs continues to grow in terms of market capitalization and product diversity, there are plenty of new problems for future research. The availability of high-frequency trading data also permits the analysis of the intraday return patterns and tracking performance of these funds compared to their reference assets.
In Fall 2016, I supervised six students for a project called "Mathematics of Exchange-Traded Funds" in the Washington Experimental Mathematics Lab. It was a very rewarding experience as we were able to not only obtain new findings, but also generate new ideas for future research. I am certainly excited to continue to work with many UW undergraduate and graduate students on my research projects in years to come.
