By Tom Trogdon
I (re)joined the University of Washington in July 2019 as an Associate Professor. I originally joined the Department of Applied Mathematics during the 2008-2009 academic year as an MSc student. The following year I joined the PhD program and graduated in 2013 under the supervision of Bernard Deconinck. So, you could say, my former boss is once again my boss.
After I left UW in 2013, I spent three years at the Courant Institute of Mathematical Sciences at New York University as an NSF Postdoc. I worked with a handful of people there but my focus was on work with Percy Deift, understanding connections between random matrix theory and algorithms from numerical linear algebra.
I then joined the University of California, Irvine in 2016 as an Assistant Professor of Mathematics. During this time I was awarded an NSF CAREER award, funding additional work on numerical linear algebra and random matrix theory.
It is a true pleasure and a distinct honor to bring my work back to the UW Amath department and to the Algorithmic Foundations of Data Science Institute where I am an affiliate member. And while the socially distant winter and spring quarters have hindered collaboration with my colleagues, I do look forward to addressing interesting problems at the intersection of my expertise and other specialties within the department, including data science, optimization and neuroscience.
A recap of a year at UW
An important feature that pulled me back to UW Amath is the strength, passion and ambition of the graduate students here. I am currently co-advising two UW Amath students on very different projects: Xin Yang (with Bernard Deconinck) is working on numerical aspects of initial-boundary value problems for nonlinear wave equations and Tyler Chen (with Anne Greenbaum) is working with me on problems at the intersection of random matrix theory and Krylov subspace methods.
As for teaching this last year, I had the privilege to both teach a course I have already taught as a graduate student (Amath 352) and to teach a course I took from Randy LeVeque (Amath 586). Additionally, it was particularly nice to get the opportunity to teach the numerical solution of PDEs in Julia (https://julialang.org).
Also, of note in the last year, in collaboration with Sheehan Olver (Imperial College London), I gave a Masterclass at the Isaac Newton Institute on the numerical solution of Riemann-Hilbert problems. Riemann-Hilbert problems are an interesting class of boundary-value problems in the complex plane that, on one hand, represent a powerful tool for analysis and, on the other hand, give a means of connecting the mathematical areas of special functions, orthogonal polynomials, inverse problems, integrable systems and random matrices.
Research
To give a flavor of the type of questions I am interested in as of late, consider the problem of solving the least-squares problem
A x ≈ b,
where A is a full rank m x n matrix, m > n. The solution of this problem is, of course, given by the solution of the normal equations
ATA x = ATb.
To solve this linear system of equations, one approach is to apply the conjugate gradient algorithm (CGA). Now, supposing that A is random, with independent (mean zero, variance one) entries, ignoring some technical moment conditions, we have established that
Relative error at iteration k ≈ dk/2 (1 - d)1/2 (1 - dk+1)-1/2, d = n/m,
if n is sufficiently large. There are a few, in my opinion, remarkable features of this relation. The first is that the relation is only influenced by the mean and the variance, i.e., it is a universal formula and it holds for a wide class of distributions on the entries of A. The second feature is that it is a deterministic quantity. For large matrices and k = O(1), the errors behave almost deterministically. Lastly, as displayed in Figure 1, the number of needed iterations of the CGA to achieve a prescribed error tolerance ε tends to a deterministic value as the matrix size grows.
The results go beyond this, establishing a central limit theorem for the errors. This work is joint with Elliot Paquette (OSU). A preprint for this can be found here: https://arxiv.org/abs/2007.00640 .
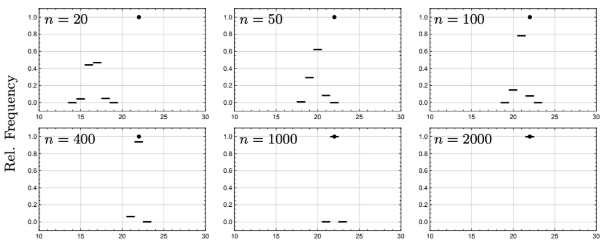
Iteration count
Figure 1: A demonstration that the number of iterations to achieve a prescribed error tolerance ε becomes almost deterministic as n increases for d = 1/5 using 20,000 samples. Each panel gives the histogram for the number of iterations required to achieve an error less than ε when the CGA is applied to a random linear system. The dot represents the limiting value for this histogram. For n sufficiently large, n ≥ 2000, the histogram is extremely concentrated at 22 iterations despite the fact that the matrix A is random (taken from https://arxiv.org/abs/1901.09007).
Similar questions can be asked about a variety of algorithms and it is important to understand how things behave if the assumptions on A are modified. Results of this type give indications of the efficacy of iterative algorithms for problems that arise in data science.
Reflections on UW
Returning to UW compels me to contemplate the national and global influence of the UW Amath department and mathematics at UW as a whole. So often in my previous positions, colleagues would sing the praises of the UW Amath department. It makes me so proud to represent it.
But maybe no example of the quality educational opportunities that UW provides is better than that of one of my newly-formed collaborations. I met my now collaborator, Elliot Paquette, during TA training at UW! He was a student of Ioana Dumitriu in the Department of Mathematics. Elliot and I overlapped again at the Courant Institute during our respective postdoc appointments when he visited regularly from the Weizmann Institute. We ended up writing our aforementioned paper on “Universality for the conjugate gradient and MINRES algorithms on sample covariance matrices”. We should all be open to new professional relationships at every stage of our careers!